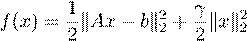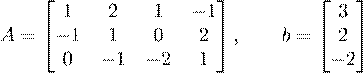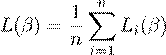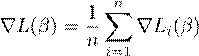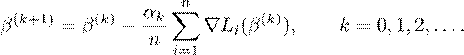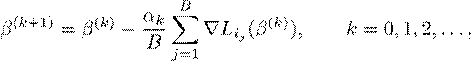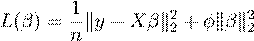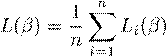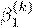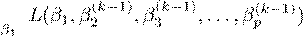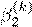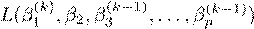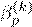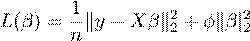Starting from:

$30

COMP9417 - Machine Learning

Homework 1: Regularized Regression & Numerical

Optimization

Introduction In this homework we will explore some algorithms for gradient based optimization. These algorithms have been crucial to the development of machine learning in the last few decades. The most famous example is the backpropagation algorithm used in deep learning, which is in fact just an application of a simple algorithm known as (stochastic) gradient descent. We will first implement gradient descent from scratch on a deterministic problem (no data), and then extend our implementation to solve a real world regression problem.

Points Allocation There are a total of 28 marks.

Question 1 a): 2 marks

Question 1 b): 1 mark

Question 1 c): 4 marks

Question 1 d): 1 mark

Question 1 e): 1 mark

Question 1 f): 2 marks

Question 1 g): 3 marks

Question 1 h): 3 marks

Question 1 i): 1 mark

Question 1 j): 4 marks

Question 1 k): 5 marks

Question 1 l): 1 mark

What to Submit

A single PDF file which contains solutions to each question. For each question, provide your solution in the form of text and requested plots. For some questions you will be requested to provide screen shots of code used to generate your answer — only include these when they are explicitly asked for.

.py file(s) containing all code you used for the project, which should be provided in a separate .zip file. This code must match the code provided in the report.

You may be deducted points for not following these instructions.

You may be deducted points for poorly presented/formatted work. Please be neat and make your solutions clear. Start each question on a new page if necessary.

You cannot submit a Jupyter notebook; this will receive a mark of zero. This does not stop you from developing your code in a notebook and then copying it into a .py file though, or using a tool such as nbconvert or similar.

We will set up a Moodle forum for questions about this homework. Please read the existing questions before posting new questions. Please do some basic research online before posting questions. Please only post clarification questions. Any questions deemed to be fishing for answers will be ignored and/or deleted.

Please check Moodle announcements for updates to this spec. It is your responsibility to check for announcements about the spec.

Please complete your homework on your own, do not discuss your solution with other people in the course. General discussion of the problems is fine, but you must write out your own solution and acknowledge if you discussed any of the problems in your submission (including their name(s) and zID).

As usual, we monitor all online forums such as Chegg, StackExchange, etc. Posting homework questions on these site is equivalent to plagiarism and will result in a case of academic misconduct.

You may not use SymPy or any other symbolic programming toolkits to answer the derivation questions. This will result in an automatic grade of zero for the relevant question. You must do the derivations manually.

When and Where to Submit

Due date: Week 4, Monday June 20th, 2022 by 5pm. Please note that the forum will not be actively monitored on weekends.

Late submissions will incur a penalty of 5% per day from the maximum achievable grade. For example, if you achieve a grade of 80/100 but you submitted 3 days late, then your final grade will be 80 − 3 × 5 = 65. Submissions that are more than 5 days late will receive a mark of zero.

Submission must be done through Moodle, no exceptions.

Question 1. Gradient Based Optimization

The general framework for a gradient method for finding a minimizer of a function f : Rⁿ→ R is defined by

x^(k+1)= x^(k)− α_k∇f(x_k), k = 0,1,2,..., (1)

where α_k> 0 is known as the step size, or learning rate. Consider the following simple example of√

minimizing the function g(x) = 2 x³+ 1. We first note that g⁰(x) = 3x²(x³+ 1)^−1/2. We then need to choose a starting value of x, say x⁽⁰⁾= 1. Let’s also take the step size to be constant, α_k= α = 0.1. Then we have the following iterations:

x⁽¹⁾= x⁽⁰⁾− 0.1 × 3(x⁽⁰⁾)²((x⁽⁰⁾)³+ 1)^−1/2= 0.7878679656440357 x⁽²⁾= x⁽¹⁾− 0.1 × 3(x⁽¹⁾)²((x⁽¹⁾)³+ 1)^−1/2= 0.6352617090300827

x⁽³⁾= 0.5272505146487477

...

and this continues until we terminate the algorithm (as a quick exercise for your own benefit, code this up and compare it to the true minimum of the function which is x_∗= −1). This idea works for functions that have vector valued inputs, which is often the case in machine learning. For example, when we minimize a loss function we do so with respect to a weight vector, β. When we take the stepsize to be constant at each iteration, this algorithm is known as gradient descent. For the entirety of this question, do not use any existing implementations of gradient methods, doing so will result in an automatic mark of zero for the entire question. (a) Consider the following optimisation problem:

min f(x), x∈Rⁿ

where

and where A ∈ R^m^×n, b ∈ R^mare defined as

and γ is a positive constant. Run gradient descent on f using a step size of α = 0.1 and γ = 0.2 and starting point of x⁽⁰⁾= (1,1,1,1). You will need to terminate the algorithm when the following condition is met: k∇f(x^(k))k₂< 0.001. In your answer, clearly write down the version of the gradient steps (1) for this problem. Also, print out the first 5 and last 5 values of x^(k), clearly indicating the value of k, in the form:

k = 0,	x^(k)= [1,1,1,1]
k = 1,	x(k) = ···
k = 2,	x(k) = ···

...

What to submit: an equation outlining the explicit gradient update, a print out of the first 5 (k = 5 inclusive) and last 5 rows of your iterations. Use the round function to round your numbers to 4 decimal places. Include a screen shot of any code used for this section and a copy of your python code in solutions.py.

In the previous part, we used the termination condition k∇f(x^(k))k₂< 0.001. What do you think this condition means in terms of convergence of the algorithm to a minimizer of f ? How would making the right hand side smaller (say 0.0001) instead, change the output of the algorithm? Explain.

What to submit: some commentary.

In lab 2, we introduced PyTorch and discussed how to use it to perform gradient descent. In this question you will replicate your previous analysis in part (a) but using PyTorch instead. As in part (a), clearly write down the version of the gradient steps (1) for this problem. Also, print out the first 5 and last 5 values of x^(k), clearly indicating the value of k. You may use the following code as a template if you find it helpful. Note that you may not make any calls to NumPy here.

import torch import torch.nn as nn from torch import optim

A = ### b = ### tol = ### gamma = 0.2 alpha = 0.1

class MyModel(nn.Module):

def __init__(self): super().__init__() self.x = ####

def forward(self, ###):

return ###

model = MyModel() optimizer = ### terminationCond = False

k = 0 while not terminationCond:

### compute loss, find gradients, update, check termination cond. etc

What to submit: a print out of the first 5 (k = 5 inclusive) and last 5 rows of your iterations. Use the round function to round your numbers to 4 decimal places. Include a screen shot of any code used for this section and a copy of your python code in solutions.py.

In the next few parts, we will use gradient methods explored above to solve a real machine learning problem. Consider the CarSeats data provided in CarSeats.csv. It contains 400 observations with each observation describing child car seats for sale at one of 400 stores. The features in the data set are outlined below:

Sales: Unit sales (in thousands) at each location

CompPrice: Price charged by competitor at each location

Income: Local income level (in thousands of dollars)

Advertising: advertising budget (in thousands of dollars)

Population: local population size (in thousands)

Price: price charged by store at each site

ShelveLoc: A categorical variable with Bad, Good and Medium describing the quality of the shelf location of the car seat

Age: Average age of the local population

Education: Education level at each location

Urban A categorical variable with levels No and Yes to describe whether the store is in an urban location or in a rural one

US: A categorical variable with levels No and Yes to describe whether the store is in the US or not.

The target variable is Sales. The goal is to learn to predict the amount of Sales as a function of a subset of the above features. We will do so by running Ridge Regression (Ridge) which is defined as follows

βˆRidge = argmin ,

where β ∈ R^p,X ∈ Rⁿ^×p,y ∈ Rⁿand φ > 0.

We first need to preprocess the data. Remove all categorical features. Then use sklearn.preprocessing.StandardScaler to standardize the remaining features. Print out the mean and variance of each of the standardized features. Next, center the target variable (subtract its mean). Finally, create a training set from the first half of the resulting dataset, and a test set from the remaining half and call these objects X train, X test, Y train and Y test. Print out the first and last rows of each of these.

What to submit: a print out of the means and variances of features, a print out of the first and last rows of the 4 requested objects, and some commentary. Include a screen shot of any code used for this section and a copy of your python code in solutions.py.

It should be obvious that a closed form expression for β^ˆ_Ridgeexists. Write down the closed form expression, and compute the exact numerical value on the training dataset with φ = 0.5. What to submit: Your working, and a print out of the value of the ridge solution based on (X train, Y train). Include a screen shot of any code used for this section and a copy of your python code in solutions.py.

We will now solve the ridge problem but using numerical techniques. As noted in the lectures, there are a few variants of gradient descent that we will briefly outline here. Recall that in gradient descent our update rule is

β(k+1) = β(k) − αk∇L(β(k)), k = 0,1,2,...,

where L(β) is the loss function that we are trying to minimize. In machine learning, it is often the case that the loss function takes the form

i.e. the loss is an average of n functions that we have lablled L_i. It then follows that the gradient is also an average of the form

We can now define some popular variants of gradient descent .

Gradient Descent (GD) (also referred to as batch gradient descent): here we use the full gradient, as in we take the average over all n terms, so our update rule is:

Stochastic Gradient Descent (SGD): instead of considering all n terms, at the k-th step we choose an index i_krandomly from {1,...,n}, and update

β(k+1) = β(k) − αk∇Lik(β(k)), k = 0,1,2,....

Here, we are approximating the full gradient ∇L(β) using ∇L_i_k(β).

Mini-Batch Gradient Descent: GD (using all terms) and SGD (using a single term) represents the two possible extremes. In mini-batch GD we choose batches of size 1 < B < n randomly at each step, call their indices {i_k₁,i_k₂,...,i_k_B}, and then we update

so we are still approximating the full gradient but using more than a single element as is done in SGD.

The ridge regression loss is

Show that we can write

and identify the functions L₁(β),...,L_n(β). Further, compute the gradients ∇L₁(β),...,∇L_n(β) What to submit: your working.

In this question, you will implement (batch) GD from scratch to solve the ridge regression problem. Use an initial estimate β⁽⁰⁾= 1_p(the vector of ones), and φ = 0.5 and run the algorithm for 1000 epochs (an epoch is one pass over the entire data, so a single GD step). Repeat this for the following step sizes:

α ∈ {0.000001,0.000005,0.00001,0.00005,0.0001,0.0005,0.001,0.005,0.01}

To monitor the performance of the algorithm, we will plot the value

∆(k) = L(β(k)) − L(βˆ),

where β^ˆis the true (closed form) ridge solution derived earlier. Present your results in a 3 × 3 grid plot, with each subplot showing the progression of ∆^(k)when running GD with a specific step-size. State which step-size you think is best and let β^(K)denote the estimator achieved when running GD with that choice of step size. Report the following:

The train MSE:

The test MSE:

What to submit: a single plot, the train and test MSE requested. Include a screen shot of any code used for this section and a copy of your python code in solutions.py.

We will now implement SGD from scratch to solve the ridge regression problem. Use an initial estimate β⁽⁰⁾= 1_p(the vector of ones) and φ = 0.5 and run the algorithm for 5 epochs (this means a total of 5n updates of β, where n is the size of the training set). Repeat this for the following step sizes:

α ∈ {0.000001,0.000005,0.00001,0.00005,0.0001,0.0005,0.001,0.006,0.02}

Present an analogous 3 × 3 grid plot as in the previous question. Instead of choosing an index randomly at each step of SGD, we will cycle through the observations in the order they are stored in X train to ensure consistent results. Report the best step-size choice and the corresponding train and test MSEs. In some cases you might observe that the value of ∆^(k)jumps up and down, and this is not something you would have seen using batch GD. Why do you think this might be happening?

What to submit: a single plot, the train and test MSE requested and some commentary. Include a screen shot of any code used for this section and a copy of your python code in solutions.py.

Based on your GD and SGD results, which algorithm do you prefer? When is it a better idea to use GD? When is it a better idea to use SGD?

Note that in GD, SGD and mini-batch GD, we always update the entire p-dimensional vector β at each iteration. An alternative popular approach is to update each of the p parameters individually. To make this idea more clear, we write the ridge loss L(β) as L(β₁,β₂...,β_p). We initialize β⁽⁰⁾, and then solve for k = 1,2,3,...,

= argmin

β₂

...

= argmin.

β_p

Note that each of the minimizations is over a single (1-dimensional) coordinate of β, and also that as as soon as we update, we use the new value when solving the update for and so on. The idea is then to cycle through these coordinate level updates until convergence. In the next two parts we will implement this algorithm from scratch for the Ridge regression problem:

Note that we can write the n × p matrix X = [X₁,...,X_p], where X_jis the j-th column of X. Find the solution of the optimization

β^ˆ₁= argminL(β₁,β₂,...,β_p).

β₁

Based on this, derive similar expressions for β^ˆ_jfor j = 2,3,...,p.

Hint: Note the expansion: Xβ = X_jβ_j+ X_−jβ_−j, where X_−jdenotes the matrix X but with the j-th column removed, and similarly β_−jis the vector β with the j-th coordinate removed. What to submit: your working out.

Implement the algorithm outlined in the previous question on the training dataset. In your implementation, be sure to update the β_j’s in order and use an initial estimate of β⁽⁰⁾= 1_p(th vector of ones), and φ = 0.5. Terminate the algorithm after 10 cycles (one cycle here is p updates, one for each β_j), so you will have a total of 10p updates. Report the train and test MSE of your resulting model. Here we would like to compare the three algorithms: new algorithm to batch GD and SGD from your previous answers with optimally chosen step sizes. Create a plot of k vs. ∆^(k)as before, but this time plot the progression of the three algorithms. Be sure to use the same colors as indicated here in your plot, and add a legend that labels each series clearly. For your batch GD and SGD include the step-size in the legend. Your x-axis only needs to range from k = 1,...10p. Further, report both train and test MSE for your new algorithm. Note: Some of you may be concerned that we are comparing one step of GD to one step of SGD and the new aglorithm, we will ignore this technicality for the time being. What to submit: a single plot, the train and test MSE requested.

In part (d), we standardized the entire data set and then split into train and test sets. In light of this, do you believe that your results in parts (e)-(k) are more reliable, less reliable, or unaffected?

Explain. What to submit: your commentary